Pomiar postaci geometrycznej przedmiotu ma na celu sprawdzenie, czy ustalone przez konstruktora wymagania zostały spełnione. Tolerancje geometryczne są znormalizowane. Zawarte są w normach GPS, czyli w specyfikacji geometrii wyrobów (ang. Geometrical Product Specifications, GPS). Pozwalają one odzwierciedlić rozpatrywany element w złożeniu, czyli zdefiniować na rysunku tolerancje w taki sposób, że kiedy zostaną one spełnione część będzie montowalna z wystarczającą dokładnością, określoną przez konstruktora na etapie projektowania. Inspekcję elementów zgodnie z nowoczesną dokumentacja techniczną umożliwiają współrzędnościowe maszyny pomiarowe. Jest to rozwiązanie, które w szybki i relatywnie prosty sposób pozwala dokonać pełnej kontroli wszystkich wymiarów geometrycznych elementu.
Współrzędnościowa technika pomiarowa (WTP) z definicji jest dedykowana do pomiarów w odniesieniu do układu współrzędnych. Celem pomiarów, jest uzyskanie punktów o określonych współrzędnych, które następnie będą mogły zostać poddane analizie. Technologia ta, umożliwia inspekcję wszystkich cech opisanych na rysunku technicznym, pod warunkiem wystarczającej dokładności maszyny pomiarowej oraz zastosowania odpowiedniego osprzętu.
Przestrzenny element maszynowy w rzeczywistości składa się prostych figur płaskich i elementów takich jak: punkt, prosta, płaszczyzna, a także z figur przestrzennych: walec, stożek, kula. W procesie pomiaru wyznacza się wartości współrzędnych przestrzennych punktów zarysu przedmiotu. Znajomość położenia punktów charakterystycznych podstawowych figur umożliwia wyznaczenie odległości między nimi w postaci wymiarów – kątowych, liniowych czy tolerancji geometrycznych. Opis matematyczny prostych figur geometrycznych stanowi podstawę procedur pomiarowych WTP. Położenie punktu w układzie przestrzennym określa się na podstawie współrzędnych 𝑃[𝑥,𝑦,𝑧].
Prosta
Prosta w przestrzeni może być opisana równaniem matematycznym. Schemat opisu przedstawiono na rysunku poniżej (rys. 1). Dla konstrukcji prostej zaleca się pomiar minimum trzech punktów.
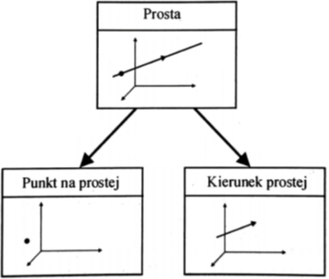
Rysunek 1 Prosta
Płaszczyzna
W celu wyznaczenia płaszczyzny stosowana jest aproksymacja punktów pomiarowych z wykorzystaniem metody najmniejszych kwadratów. Schemat konstrukcji płaszczyzny
przedstawiono poniżej (rys. 2). Zaleca się pomiar przynajmniej czterech punktów.
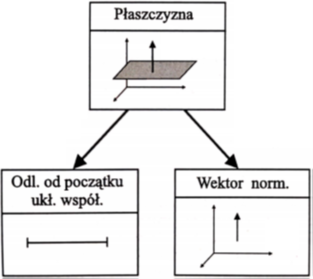
Rysunek 2 Płaszczyzna
Okrąg
Aby wyznaczyć średnicę oraz środek okręgu stosowana jest aproksymacja punktów pomiarowych metoda najmniejszych kwadratów (schemat konstrukcji – rys. 3). Dla obliczenia okręgu koniczne jest uprzednie wyznaczenie płaszczyzny odniesienia. Zaleca się pomiar co najmniej czterech punktów pomiarowych leżących na obwodzie mierzonego okręgu.
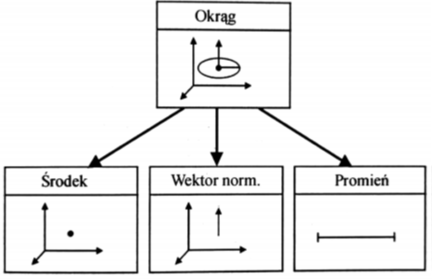
Rysunek 3 Okrąg
Kula (sfera)
Do wyznaczenia środka oraz średnicy kuli stosowana jest aproksymacja punktów pomiarowych metodą najmniejszych kwadratów. Schemat konstrukcji kuli przedstawiono na schemacie poniżej (rys. 4).
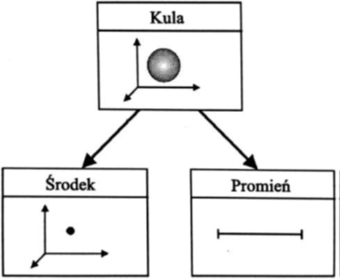
Rysunek 4 Kula (sfera)
Stożek
Cechą charakterystyczną dla stożka jest stały kąt wierzchołkowy. Stożek opisany jest poprzez szereg skomplikowanych równań nieliniowych, które rozwiązuje się metodą iteracyjną. Schemat konstrukcji przedstawiono poniżej (rys. 5).
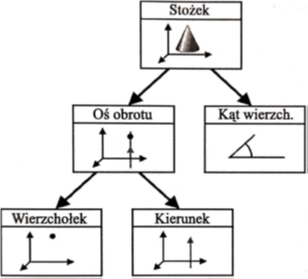
Rysunek 5 Stożek
Walec
Cechą charakterystyczną dla walca jest stała odległość punktów od prostej. Obliczenia jak w przypadku stożka oparte są na równaniach nieliniowych, a rozwiązywane są iteracyjnie. Schemat przedstawiono poniżej (rys. 6).

Rysunek 6 Walec
Niezwykle ważne jest zrozumienie sposobu budowania elementów zastępczych jakimi są proste elementy geometryczne (punkt, prosta, płaszczyzna, walec, stożek, kula) oraz zrozumienie co jest ich reprezentacją. Okrąg oraz sfera reprezentowane są za pomocą punktu. Dla walca oraz stożka jest to prosta. Mogą one jednak być budowane z uwzględnieniem różnych metod kalkulacji. Elementy mogą być budowane na podstawie uśredniania lub na zasadzie przystawania do skrajnych punktów. Na przykładzie walca najczęściej stosowanymi metodami kalkulacji elementów są: metoda najmniejszych kwadratów (gauss), największy element wpisany oraz najmniejszy opisany. Norma GPS ISO 1101 definiuje symbole modyfikatorów w zależności od oczekiwanego sposobu kalkulacji cechy:
Najmniejszy kształt opisany – N
Największy kształt wpisany – X
Funkcja najmniejszych kwadratów – G
Sposób zapisu na rysunku
Modyfikator G zapisujemy na rysunku zgodnie z poniższym oznaczeniem, w ramce tolerancji geometrycznej tuż za wartością pola tolerancji.
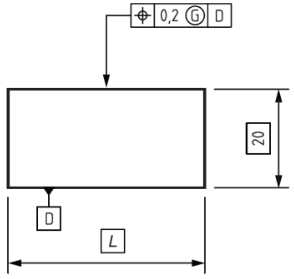
Rysunek 7 Modyfikator G – zapis
W metodzie tej minimalizuje się średnią kwadratową promieniową odległość zmierzonych punktów od linii środkowej, a następnie oblicza się wartość skuteczną.
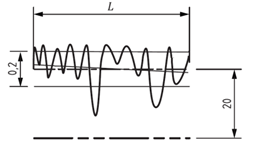
Rysunek 8 Modyfikator G – interpretacja
Modyfikator N oznacza najmniejszy kształt opisany, czyli innymi słowy, jest to średnica najmniejszej tulei o idealnym kształcie, w którą można włożyć mierzony wałek.
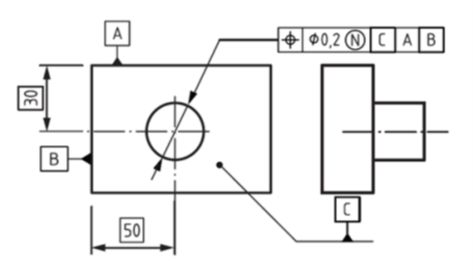
Rysunek 9 Modyfikator N – zapis
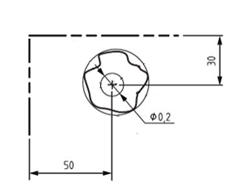
Rysunek 10 Modyfikator N – interpretacja
Modyfikator X natomiast oznacza największy kształt wpisany, czyli obrazuje największą możliwą średnicę trzpienia o idealnym kształcie, który można przełożyć przez rozpatrywany otwór.
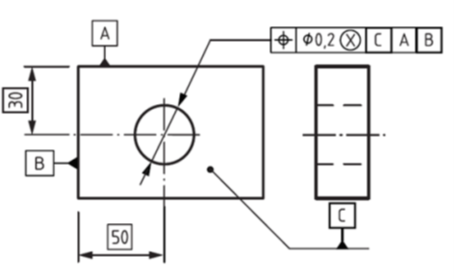
Rysunek 11 Modyfikator X – zapis
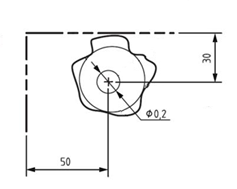
Rysunek 12 Modyfikator X – interpretacja
Elementy zastępcze i sposób ich kalkulacji to prawdopodobnie najważniejszy aspekt metrologii współrzędnościowej. Programista podczas przygotowania programu do inspekcji musi najpierw zastanowić się jakim elementem zastępczym może opisać mierzoną cechę, a następnie podjąć decyzję o sposobie kalkulacji. Dlaczego sposób kalkulacji jest tak istotny? Ponieważ zmienia położenie elementu zastępczego. W innym miejscu zlokalizowany będzie środek okręgu zmierzonego i obliczonego metodą najmniejszych kwadratów, w innym jeśli programista użyje elementu wpisanego, oraz w innym jeśli będzie to element opisany na zmierzonych punktach. Te cechy z kolei będą miały fundamentalny wpływ na zbudowany na nich układ współrzędnych i wyniki rozpatrywanych względem nich cech mierzonego obiektu. Właściwa kalkulacja elementów ma bezpośredni wpływ na jakość przeprowadzonych pomiarów i jest jednocześnie jednym z najczęściej popełnianych błędów.